寒鸽儿のBlog

寒鸽儿gugugu~

首页 归档 标签 关于

笔记 自适应辛普森积分

2020-03-09 13 min read # 模板 # 数学 # 笔记

辛普森积分用于计算∫abf(x)dx\mathcal{\int_{a}^{b}f(x)dx}。

前置知识

定积分的概念

定积分表示函数f(x)f(x)在某个区间上的极限和, 直观地讲, 它表示在二维平面上函数曲线、直线、x轴围成的曲边梯形的面积大小。

积分的可加性

若f(x)f(x)在区间[a,c][a, c]上是可积的, 且a⩽b⩽ca \leqslant b \leqslant c, 则有

∫abf(x)dx+∫bcf(x)dx=∫acf(x)dx\displaystyle \mathcal{\int_{a}^{b}f(x)dx} + \displaystyle \mathcal{\int_{b}^{c}f(x)dx} = \displaystyle \mathcal{\int_{a}^{c}f(x)dx}

三点辛普森值

对于一个自变量区间[l,r][l, r], 我们将

f(l)+f(r)+4f(l+r2)6\displaystyle \frac{f(l) + f(r) + 4f(\frac{l+r}{2})}{6}

定义为其三点辛普森值。

辛普森积分与辛普森法

辛普森积分认为, 当b−ab - a趋向00的时候，某函数在[a,b][a, b]上的积分近似于其三点辛普森值常函数在这个区间上的积分。即

∫abf(x)dx≐(r−l)f(l)+f(r)+f(l+r2)6\displaystyle \int_{a}^{b}f(x)dx \doteq (r-l)\frac{f(l) + f(r) + f(\frac{l+r}{2})}{6}

其中 (r−l)f(l)+f(r)+f(l+r2)6(r-l)\frac{f(l) + f(r) + f(\frac{l+r}{2})}{6}称为辛普森积分值。故可以将原区间等分为很多小段, 求出辛普森积分值然后相加得到积分的近似值。平均情况下，划分的小段长度越短, 用这个方法求得的近似值与原值越接近, 该方法精度越高。
但是这样做会遇到问题, 我们并不知道划分为多少段才能够达到我们要求的精度。在有些函数上, 并不需要划分得过密, 例如一次函数无论划分多少段其辛普森积分值都严格等于该函数的积分值, 在某些二阶导数很大(即“变化”程度很大)的函数上则需要划分很多段才能取得较高精度的近似解。此外, 在同一函数上的“变化”程度也会不同。这意味着, 笼统的划分一方面将使我们在许多不必要的地方浪费时间(并且过度划分可能会因为浮点数运算过多降低精度), 另一方面在必要的地方计算不足而使得结果的精度不高。

自适应辛普森法

好在辛普森法有一个“自适应”的版本。
我们记S(l,r)S(l, r)为区间[l,r][l, r]上的辛普森积分值。如果满足

∣S(l,l+r2)+S(l+r2,r)−S(l,r)∣⩽15eps|S(l, \frac{l+r}{2}) + S(\frac{l+r}{2}, r) - S(l, r)| \leqslant 15eps

我们认为这个划分在精度epseps下取得的辛普森积分值等于原来函数的积分值。
那么算法的流程就清晰了, 如果精度足够就直接返回辛普森积分值, 如果精度不够, 就不断递归进行划分, 直到精度足够。

注意点:

  1. 实际上double计算时也会有误差, 所以一般把精度设得更高一些。
  2. 向下递归时, eps/=2eps /= 2。
  3. 由经验规律, 通常在精度足够时将返回值加上S(l,l+r2)+S(l+r2,r)−S(l,r)15\frac{S(l, \frac{l+r}{2}) + S(\frac{l+r}{2}, r) - S(l, r)}{15}, 即S(l,l+r2)+S(l+r2,r)+S(l,l+r2)+S(l+r2,r)−S(l,r)15S(l, \frac{l+r}{2}) + S(\frac{l+r}{2}, r) + \frac{S(l, \frac{l+r}{2}) + S(\frac{l+r}{2}, r) - S(l, r)}{15}

板子代码

(Luogu P4525)

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

double a, b, c, d;
inline double f(double x) { // 原函数求值, 可替换
	return (c * x + d) / (a * x + b);
}

inline double simpson(double l, double r) {
	return (f(l) + 4 * f(0.5*(l+r)) + f(r)) * (r - l) / 6;
}

double asr(double l, double r, double eps, double la) {
	double mid = 0.5 * (l + r);
	double ls = simpson(l, mid), rs = simpson(mid, r);
	if(abs(ls + rs - la) <= 15 * eps) return ls + rs + (rs + ls - la) / 15;
	return asr(l, mid, eps * 0.5, ls) + asr(mid, r, eps * 0.5, rs);
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	double l, r;
	cin >> a >> b >> c >> d >> l >> r;
	cout.setf(ios::fixed);
	cout.precision(6);
	cout << asr(l, r, 1e-6, simpson(l, r)) << '\n';
	return 0;
}

(luogu P4526)
a<0a < 0不收敛输出"orz".
a⩾0a \geqslant 0收敛, 在自变量较大的地方趋近于0直接忽略掉, 跑simpson即可。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

double a;
inline double f(double x) {
	return pow(x, a / x - x); 
}

inline double simpson(double l, double r) {
	return (f(l) + 4 * f(0.5*(l+r)) + f(r)) * (r - l) / 6;
}

double asr(double l, double r, double eps, double la) {
	double mid = 0.5 * (l + r);
	double ls = simpson(l, mid), rs = simpson(mid, r);
	if(abs(ls + rs - la) <= 15 * eps) return ls + rs;
	return asr(l, mid, eps * 0.5, ls) + asr(mid, r, eps * 0.5, rs);
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin >> a;
	if(a < 0) cout << "orz\n";
	else {
		cout.setf(ios::fixed);
		cout.precision(5);
		cout << asr(1e-8, 20, 1e-8, simpson(1e-8, 20)) << '\n';
	}
	return 0;
}

习题

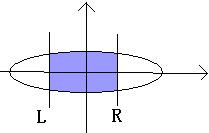
(1) HDU1724 Ellipse

对一个中心在原点的椭圆, 求如图蓝色区域面积。

裸题, 由椭圆标准方程

x2a2+y2b2=1\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1

化出上半边的式子

y=b1−x2a2\displaystyle y = b\sqrt{1-\frac{x^2}{a^2}}

然后乘2即得面积。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

double a, b, a2;

double f(double x) {
	return 2 * b * sqrt(1 - (x*x) / a2);	
}

inline double simpson(double l, double r) {
	return (r - l) * (f(l) + f(r) + 4 * f(0.5 * (l + r))) / 6;
}

double asr(double l, double r, double eps, double la) {
	double mid = 0.5 * (l + r);
	double ls = simpson(l, mid), rs = simpson(mid, r);
	if(abs(ls + rs - la) <= 15 * eps) return ls + rs + (ls + rs - la) / 15;
	return asr(l, mid, 0.5 * eps, ls) + asr(mid, r, 0.5 * eps, rs);
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.setf(ios::fixed);
	cout.precision(3);
	double l, r;
	int n;
	cin >> n;
	while(n--) {
		cin >> a >> b >> l >> r;
		a2 = a * a;
		cout << asr(l, r, 1e-5, simpson(l, r)) << '\n';
	}
	return 0;
}
(2) BZOJ 2178 圆的面积并

给定nn个圆, n⩽1000n \leqslant 1000， 坐标范围在[−1000,1000][-1000, 1000]。求圆的面积并。
计算几何题, 按交点分割成多边形和弧形, 代码又臭又长。
但是可以用simpson水过去。计算某个坐标上的所有圆的截线段并的长度作为函数值、将圆的横坐标覆盖的区间范围作为自变量的范围求积分相加即可。
一个小trick: 实际上在之前的计算中同一个函数值被计算了很多次, 在这里函数值计算的代价很大, 考虑算出来之后把值记下来, 使每一个值只被算一遍。
BZOJ好像有一组数据来卡这个做法, 限制一下递归层数, 大概强制递归10层就不会漏掉。

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

struct circ {
	double x, y, r;
	circ(){}
	circ(int X, int Y, int R) : x(X), y(Y), r(R) {}
};

struct seg {
	double l, r;
	seg() {}
	seg(double L, double R) : l(L), r(R) {}
}sgs[1010];

circ circs[1010], tmp[1010];
int isen[1010], ed = 0;

double f(double x) {
	vector<seg> v;
	for(int i = 0; i < ed; ++i) {
		circ& cur = circs[i]; 
		if(cur.x - cur.r < x && cur.x + cur.r > x) {
			double dl = sqrt(cur.r * cur.r - (cur.x-x) * (cur.x-x));
			v.push_back(seg(cur.y - dl, cur.y + dl));
		}
	} 
	if(v.empty()) return 0;
	sort(v.begin(), v.end(), [&](seg a, seg b){ return a.l < b.l; });
	double ans = v[0].r - v[0].l, nr = v[0].r;
	int vs = v.size(); 
	for(int i = 1; i < vs; ++i)
		if(v[i].r > nr) ans += v[i].r - max(nr, v[i].l), nr = v[i].r;
	return ans;
}

inline double simpson(double l, double r, double fl, double fmid, double fr) {
	return (r - l) * (fl + fr + 4 * fmid) / 6;
}

double asr(double l, double r, double fl, double fmid, double fr, double la, int d) {
	double mid = 0.5 * (l + r);
	double flmid = f(0.5*(l+mid)), frmid = f(0.5*(mid+r));
	double ls = simpson(l, mid, fl, flmid, fmid), rs = simpson(mid, r, fmid, frmid, fr);
	if(abs(ls + rs - la) <= 1e-8 && d > 10) return la;
	return asr(l, mid, fl, flmid, fmid, ls, d+1) + asr(mid, r, fmid, frmid, fr, rs, d+1);
}

inline double dis2(double x1, double y1, double x2, double y2) {
	return (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2);
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.setf(ios::fixed);
	cout.precision(3);
	int n;
	double tx, ty, tr;
	cin >> n;
	for(int i = 0; i < n; ++i) {
		cin >> tx >> ty >> tr;
		tmp[i] = circ(tx, ty, tr);
	}
	for(int i = 0; i < n; ++i)
		for(int j = i + 1; j < n; ++j) 
			if(dis2(tmp[i].x, tmp[i].y, tmp[j].x, tmp[j].y) <= (tmp[i].r-tmp[j].r)*(tmp[i].r-tmp[j].r)) {
				if(tmp[i].r < tmp[j].r) isen[i] = 1;
				else isen[j] = 1;
				break;
			}
	for(int i = 0; i < n; ++i)
		if(!isen[i])
			circs[ed] = tmp[i], sgs[ed++] = seg(tmp[i].x-tmp[i].r, tmp[i].x+tmp[i].r);
	sort(sgs, sgs+ed, [&](seg x, seg y){ return x.l < y.l; });
	double l = sgs[0].l, r = sgs[0].r, ans;
	for(int i = 1; i < ed; ++i) {
		if(sgs[i].l > r) {
			double fl = f(l), fr = f(r), fmid = f(0.5*(l+r));
			ans	+= asr(l, r, fl, fmid, fr, simpson(l, r, fl, fmid, fr), 0);
			l = sgs[i].l, r = sgs[i].r;
		} else r = max(sgs[i].r, r);
	}
	double fl = f(l), fr = f(r), fmid = f(0.5*(l+r));
	ans	+= asr(l, r, fl, fmid, fr, simpson(l, r, fl, fmid, fr), 0);
	cout << ans << '\n';
	return 0;
}

参考资料

刘汝佳 《算法竞赛入门经典(训练指南) 第2版》

Powered by Gridea RSS